巡回行列と対称行列についての自作定理

訂正:故に(^t)A'＝A'

層の直観的描像

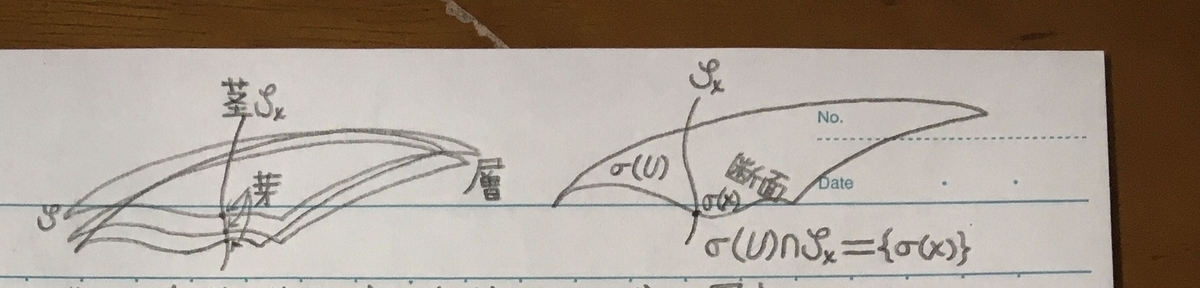
位相空間M上の加法群の層とは, 位相空間Sと写像π:S→Mから成る組(S, π, M)または単にSで,

πは局所位相同型写像であり

各点p∈Mに対しS_p＝(π^(−1))(p)⊆Sは加法群であり,

加法はSの位相に関して或る意味で連続である

を満たす物である. ここで, πが局所位相同型写像であるとは, 各点s∈Sに対してsの近傍V⊆Sとπ(s)の近傍U⊆Mが存在してπのVへの制限が位相同型写像, すなわちπ|V:V→Uが位相同型写像となることである.

S_pを層Sの茎, πを射影という.

他の代数的構造の入った層の定義も同様である.

(S, π, M)を層, U⊆Mを開集合とする. 連続写像σ:U→Sは∀x∈U, π(σ(x))＝xを満たすときU上のSの切断, σ(U)は切断面と呼ばれる.

代数的構造の入った位相空間M上の層Sは局所同相写像π:S→XによるSの点sの近傍V(s)の像π(V(s))をπ^(−1)|V(s)で重ねて作られたシートV(s)の集まり{V(s)|s∈Ｓ}とみなせる. 切断σ:U→Sは適当なSの点の近傍Vに対するシートσ(U)⊆Vを取り出す操作とみなせる. σとπの合成がU上の恒等写像なのは, シートσ(U)を取り出してまた入れたら, もとに戻るという取り決めだと解釈できる. 茎S_p＝(π^(−1))(p)は射影πの「逆写像」による, 層SのシートたちV(π^(−1)(p))にわたる線状の影と言える.

層は多変数複素解析や複素幾何でも多々用いられる.

数学における表現の簡略化について

数学では, 話者や読者の論理に高い厳密性が問われる. しかし, 数学において, 話者または読者の少なくとも一方がそれを破り, 表現を見やすく伝わりやすくすることがある.

例えば https://pdem.hatenadiary.com/entry/2020/10/10/115841 でも私がしたように, 関数を, 純粋な意味での集合から集合への写像f:A→Bとするのではなく, Aの任意の元xにBの元yが対応するときのy＝f(x)と書かれる対応において, 対応fと従属変数yを同一視して, 関数をy＝y(x)とすることである. 確かに正確ではないが, 具体例を扱うときや具体例に沿った論理展開をするときは便利であり, しかも厳密性は問題にならない. リンク先にあるように常微分方程式の初等的な解法は厳密性を犠牲にしなければ説明しにくい.

また, 多様体の接空間においても, 接ベクトルとベクトル場を同じ記号で書くことがある. 例えば2次元多様体Mの点pにおける接空間(T_p)(M)は局所座標を(x, y)とするとき２つの接ベクトルから成る基底

{(∂/∂x)_p, (∂/∂y)_p}

を持つが, ここでも右下の添え字pを取って基底を

{∂/∂x, ∂/∂y}

と書くことがある. 余接空間(T_p)*(M)についても同様に, 基底を

{(dx)_p, (dy)_p}

と書く代わりに

{dx, dy}

と書くことがある. もちろんこれらはベクトル場や微分形式の正確な定義を既知とした上での表現である.

また, リーマン計量gを内積gということもある. これはリーマン計量gが各点q∈Mで定める内積g_qとgを意図的に混同しているのだが, これは突き詰めて言えば最初の例である.

微分幾何において多様体の接空間やリーマン計量は多様体それ自体と同じくらいよく出てくるのでそれに関する式もたくさん出てくるし, 高次元になればそれだけ右下の添え字pがたくさん必要だが, 後者の書き方をすると式が簡単になるのである. 例えば「2次元リーマン多様体Mの余接空間(T_p)*(M)にMのリーマン計量gから定まる内積をg'と書く」とあれば, これについて, Mの各点qに対して

(g'_q)((dx)_q, (dy)_q)

＝(g_q)((∂/∂x)_q, (∂/∂y)_q)

という式を

g'(dx, dy)＝g(∂/∂x, ∂/∂y)

と簡単に書ける上に本質が見やすい. (なお, 普通g'もgと書く. )

数学の初学者には悩ましい習慣かもしれないが, 使い慣れたら便利である. それ以上の深い意味はないが…

中2の冬に発見した数学

パスカルの三角形は0段目から4段目までは0≦n≦4に対する11^nの各位の数を並べたものでもある. 対応するのは0≦n≦4の場合だけでn≧5だと11^nの各位の数を並べてもパスカルの三角形とは対応しない. これは中2の冬に発見した. 11＝10＋1 と, 二項係数≦9となるnは0≦n≦4の場合に限られることによる.

これは「5次以上の代数方程式は代数的な解の公式を持たない」に似ている.

「数」と「数字」の違い

よく, 一般人向けに

素数とは1と自分自身以外で割り切れない数字

や,

偶数とは2で割り切れる数字

奇数とは2で割り切れない数字

という表現がされていることがある. しかしこれらは誤りである.

数は概念である. 名前はまだない. そこで「0」「1」「2」「3」…など名前をつけていくのである. 0, 1, 2, 3,…は数字という文字である. しかし数の概念自体には数字を使う必然性はない. ただ, わかりやすさ, 見やすさ, 伝わりやすさのために数を表すのに数字(や小数点や分数など)が使われているだけである. 数の概念自体は理論上は数字とは無関係なのである. 数の厳密な定義と構成を知っている人なら, 数の概念は数字を使わずとも表現できることが容易に想像できるだろう. 概念と, それを表す文字に何を使うかは関係ないのだ.

例えば, 実数の公理的定義を書こう. 便宜上0, 1という数字を使うが, これはわかりやすさのためで, o, e という文字を使っても同じである. (0, 1の性質を満たす物は一意的に定まるので0, 1と書いても良い)

実数全体の集合Rは完備な全順序体として定義される. すなわち演算＋と×, 関係≧が定義され

(∀:任意の, ∃:或る〜が存在して)

(1) ∀a, b∈R: a＋b＝b＋a

(2) ∀a, b, c∈R: (a＋b)＋c＝a＋(b＋c)

(3) ∃0∈R: ∀a∈R, a＋0＝a

(4) ∀a∈R, ∃(−a)∈R: a＋(−a)＝0

(5) ∀a, b∈R: a×b＝b×a

(6) ∀a, b, c∈R: (a×b)×c＝a×(b×c)

(7) ∃1∈R: ∀a∈R, a×1＝a

(8) ∀a∈R, a≠0 ⇒ ∃(1/a)∈R: a×(1/a)＝1

(9) 0≠1

(10) ∀a, b, c∈R: a×(b＋c)＝a×b＋a×c

(11) ∀a∈R: a≧a

(12) ∀a, b∈R, a≧b かつ b≧a ⇒ a＝b

(13) ∀a, b, c∈R, a≧b かつ b≧c ⇒ a≧c

(14) ∀a, b∈R, a≧b と b≧a の少なくとも一方が成り立つ

(15) ∀a, b, c∈R: a≧b ⇒ a＋c≧b＋c

(16) ∀a, b, c∈R, a≧b かつ c≧0 ⇒ ac≧bc

(17) Rは連続性を持つ集合である:Rの上に有界な空でない任意の部分集合は上限を持つ.

の(1)-(17)を満たす集合を実数全体の集合と定義し, その要素を実数と呼ぶのである. ペアノの公理系よりも前にこれで実数を定義し, ここから自然数を定義することもできる. 詳しくは杉浦光夫氏の「解析入門Ⅰ」を参照されたい. また「新訂版 数理解析学概論」でも自然数からの数の構成から実数の構成に至った所で実数の完備な全順序体としての定義可能性に言及している.

この中で0, 1は幸いにも通常の意味での0, 1に一致する. しかし理論上は無関係であることがわかっていただけるだろうか.

文字が概念を表すとも限らない. 例えば意味のない文字列や感情を表す文字は概念たりえない. また概念がどの文字を用いて表されるかは非本質的である. 不便だが, 漢数字を使ってもかまわないのである. 2匹の犬の「2」と数として抽象化された「2」には大きな隔たりがある. 数字とは数を表す文字であり概念ではないのだ.

こちらも参照されたい :https://pdem.hatenadiary.com/entry/36940024

0の0乗0^0＝1と定めると便利なことについて

まず, 0^0が普通の意味では定められないことの説明として, ２変数関数

f(x, y)＝x^y

が(x, y)＝(0, 0)で不連続であることを挙げることがある. 確かに実際,

lim_(x→0, y→0)0^y＝0

lim_(x→0, y→0)x^0＝1

となり, lim_(x→0, y→0)f(x, y)は存在しない. ゆえにf(0, 0)をどう定めてもf(x, y)＝x^y

は(x, y)＝(0, 0)で不連続である.

しかし以前(https://pdem.hatenadiary.com/entry/2021/04/28/063032)にも話した通り, これは0^0をこの意味で(つまりlim_(x→0, y→0)x^yとして)定義できないことを意味し, 真に0^0が定義できない理由よりは弱いのである.

しかし便宜上, 0^0＝1と定めると便利である. 例えば関数のマクローリン展開(冪級数展開)を

f(x)＝Σ a_n x^n ＝ a_0 ＋ a_1 x ＋ a_2 x^2 ＋… (収束円板の内部の任意のxに対して)

と書くとき

f(0)＝a_0

であってほしい. そのためにはn＝0のとき

a_n x^n ＝ a_0 x^0 ＝ a_0

であってほしい. これは当然x＝0でも成り立つべきだから, 0^0＝1と定めない限りはx＝0の場合を考慮して

f(x)＝a_0 ＋ Σ_(n≧1) a_n x^n

としないといけない. これは冗長である.

実は測度論でも0^0＝1と定めると, 距離空間における0次元ハウスドルフ測度が数え上げ測度になる. このことを説明しよう.

(X, d)を距離空間, AをXの部分集合とする.

Aのδ-被覆とはAの被覆 {U_i} (A⊆U_1∪U_2∪…)でU_iの直径diam(U_i)＝sup{d(x, y) | x, y∈U_i}≦δとなる物を言う. 実数s＞0に対して

((H_δ)^s)(A)＝infΣ{diam(U_i)^s | {U_i}はAのδ-被覆}

とするとδ→0のとき任意のAに対して左辺は(被覆を取る範囲が狭くなるからその下限は)単調増加するので, ∞を込めて極限(H^s)(A)が存在する. H^sをs次元ハウスドルフ外測度という. ここからカラテオドリの方法によりs次元ハウスドルフ測度が定まる. 直観的にはAに「直径がδ以下」という意味で細かい被覆を取り, 被覆をどんどん細くした極限でAの大きさを測るのである.

(日本語の本だと猪狩氏の「実解析入門」と新井「ルベーグ積分講義」と邦訳の「プリンストン解析学講義Ⅲ 実解析」しか参考にならない. )

diam(U_i)＝0のときU_iは一点から成る(U_iが異なる二点を含めば直径は正となるから).

diam(U_i)＝0, s＝0のとき, diam(U_i)^s＝1と定めれば, (H^s)(A)はAの要素の個数または∞となり, H^sは数え上げ測度になる.

数え上げ測度による数列(自然数全体の集合Nまたは整数全体の集合Zから実数体Rまたは複素数体Cへの写像としての意味)の積分は数列の項の和になる.

他にも, 順序数(https://pdem.hatenadiary.com/entry/36940024)の演算でも順序数αに対して順序数としての冪α^0＝1と定められている. (「新訂版 数理解析学概論」)

今のところ, 0^0を1と定めたことによるパラドックスは発生していない.

急減少関数が可積分であることの証明 (2022年11月25日最終訂正)

多くの本では既知または行間としている.

急減少関数の典型例:exp(−|x|^2)

注意:exp(−|x|)は急減少関数ではない.

急減少関数について詳しくはこちらを参照されたい:https://pdem.hatenadiary.com/entry/2020/12/25/170131